Binary Tree Traversal Algorithms in Java: Complete Guide to Preorder, Inorder, Postorder, and Level Order Traversals

Introduction

Binary tree traversal algorithms are fundamental techniques in computer science that allow us to systematically visit every node in a binary tree exactly once. These algorithms form the backbone of many tree-based operations and are essential for understanding more complex data structures and algorithms.

🌳 What makes tree traversal special?
Unlike linear data structures (arrays, linked lists), trees have multiple paths to reach different nodes, making the order of visitation crucial for different applications.

In this comprehensive guide, we’ll explore:

• ✅ Four major traversal algorithms with step-by-step explanations
• 🔧 Complete Java implementations ready to use
• 📊 Performance analysis and complexity comparisons
• 🎯 Real-world applications and use cases
• 💡 Best practices and optimization techniques

---

Table of Contents

1. What is Tree Traversal?
2. Types of Tree Traversal
3. Depth-First Traversals
   • Preorder Traversal
   • Inorder Traversal
   • Postorder Traversal
4. Breadth-First Traversal
5. Complete Implementation
6. Performance Analysis
7. Practical Applications
8. Comparison Guide
9. Advanced Techniques
10. Conclusion

---

What is Tree Traversal?

Tree traversal is the process of visiting each node in a tree data structure exactly once in a systematic way. Think of it as taking a tour through a family tree or organizational chart - you want to visit everyone, but the order matters depending on your purpose.

Key Characteristics:

• 📍 Systematic: Follows a consistent, predictable pattern
• ✅ Complete: Visits every node exactly once
• 🔄 Ordered: The sequence of visits matters for different applications
• ⚡ Efficient: Optimized for specific use cases

Why Traversal Order Matters:

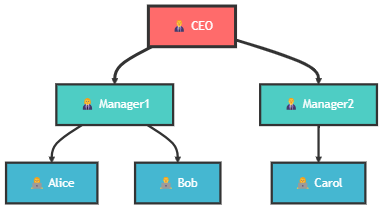
Different traversal orders serve different purposes: • Top-down: CEO → Managers → Employees (authority flow) • Bottom-up: Employees → Managers → CEO (reporting flow) • Left-to-right: Process departments in sequence

---

Types of Tree Traversal

Tree traversal algorithms can be broadly categorized into two main types:

🔽 1. Depth-First Traversal (DFS)

Explores as far as possible along each branch before backtracking.

Type	Order	Best For
Preorder	Root → Left → Right	Tree copying, prefix expressions
Inorder	Left → Root → Right	BST sorted output, expression trees
Postorder	Left → Right → Root	Tree deletion, postfix expressions

🔄 2. Breadth-First Traversal (BFS)

Explores all nodes at the current depth before moving to the next level.

Type	Order	Best For
Level Order	Level by level, left to right	Tree printing, shortest path, BFS

---

Depth-First Traversals

Depth-first traversals use a recursive approach (or stack-based iterative approach) and differ in the order they visit the current node relative to its children.

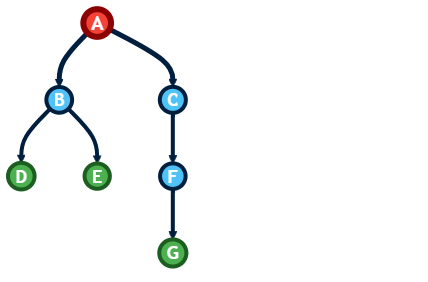
Example Tree for All Demonstrations:

---

Preorder Traversal

Preorder traversal is a type of depth-first traversal where the current node is processed first, then the left subtree, followed by the right subtree.

Order: Root → Left Subtree → Right Subtree

Think of it as: “Visit me first, then explore my left side, then my right side”

🔧 Algorithm:

preorder(node):
    if node is not null:
        visit(node)           // ✅ Process current node FIRST
        preorder(node.left)   // 🔄 Traverse left subtree
        preorder(node.right)  // 🔄 Traverse right subtree

Preorder Result: A → B → D → G → E → C → F

Use Cases & Applications:

1. Tree Copying & Cloning

Purpose: Creating an exact duplicate of a tree structure
Why Preorder: Parent nodes must be created before their children to maintain proper structure
Example:

• Input Tree: Company hierarchy with CEO → Managers → Employees
• Process: Clone CEO first, then managers under CEO, then employees under each manager
• Output: Identical organizational structure in a backup system

2. Prefix Expression Evaluation

Purpose: Processing mathematical expressions in prefix notation (Polish notation)
Why Preorder: Operators appear before operands, matching preorder’s root-first approach
Example:

• Input: + * 3 4 5 (meaning: (3 × 4) + 5)
• Process: Process ‘+’ operator first, then evaluate ‘* 3 4’, then add ‘5’
• Output: Result = 17

3. Directory & File System Traversal

Purpose: Listing folder hierarchies with directories appearing before their contents
Why Preorder: Folders must be displayed before showing what’s inside them
Example:

• Input: Project folder structure
• Process:

  📁 src/
    📁 main/
      📁 java/
        📄 Main.java
        📄 Utils.java
    📁 test/
      📄 TestMain.java
  

• Output: Hierarchical directory listing where folders appear before their files

4. Tree Serialization & Storage

Purpose: Converting tree structure to a linear format for storage or transmission
Why Preorder: Root-first order ensures proper reconstruction sequence
Example:

• Input Tree: Binary tree with nodes [A, B, C, D, E]
• Process: Serialize in preorder sequence with null markers
• Output: "A,B,D,null,null,E,null,null,C,null,null"

5. HTML/XML Document Processing

Purpose: Processing nested document structures where parent elements contain children
Why Preorder: Parent tags must be opened before processing child elements
Example:

• Input: HTML structure <div><p>Text</p><span>More</span></div>
• Process: Process <div> first, then <p>, then <span>
• Output: Properly rendered HTML with correct nesting

6. Game Scene Graph Rendering

Purpose: Rendering 3D scenes where parent transformations affect children
Why Preorder: Parent transformations must be applied before children inherit them
Example:

• Input: Character → Body → Arm → Hand hierarchy
• Process: Apply character position first, then body rotation, then arm movement
• Output: Correctly transformed 3D model where hand moves with arm and body

7. Organizational Chart Generation

Purpose: Creating visual representations of company or project hierarchies
Why Preorder: Management levels must be established before showing subordinates
Example:

• Input: Employee database with reporting relationships
• Process: Display CEO first, then VPs, then managers, then individual contributors
• Output:

  CEO: John Smith
    VP Engineering: Jane Doe
      Senior Developer: Bob Wilson
      Junior Developer: Alice Brown
    VP Marketing: Mike Johnson
  

8. Dependency Analysis & Build Systems

Purpose: Identifying what components depend on others in software projects
Why Preorder: Dependencies must be identified before they can be resolved
Example:

• Input: Module dependency tree where App → Database → Logger → FileSystem
• Process: Map dependencies starting from root application
• Output: Dependency list showing what needs to be built first: [FileSystem, Logger, Database, App]

⏱️ Complexity:

• Time: O(n) - visits each node once
• Space: O(h) - where h is tree height (recursion stack)

---

Inorder Traversal

Inorder traversal is a type of depth-first traversal where the left subtree is processed first, then the current node, followed by the right subtree.

Order: Left Subtree → Root → Right Subtree

Think of it as: “Explore my left side first, then visit me, then my right side”

Algorithm:

inorder(node):
    if node is not null:
        inorder(node.left)    // 🔄 Traverse left subtree FIRST
        visit(node)           // ✅ Process current node
        inorder(node.right)   // 🔄 Traverse right subtree

Inorder Result: G → D → B → E → A → C → F

Use Cases & Applications:

1. Binary Search Tree (BST) Data Retrieval

Purpose: Extracting data from BSTs in sorted order without additional sorting
Why Inorder: BST property ensures left < root < right, making inorder naturally sorted
Example:

• Input BST: Employee database with salary nodes [50K, 30K, 70K, 25K, 35K, 60K, 80K]
• Process: Traverse left subtree, visit root, traverse right subtree
• Output: Sorted salary list [25K, 30K, 35K, 50K, 60K, 70K, 80K]

2. Mathematical Expression Trees & Infix Conversion

Purpose: Converting expression trees to human-readable infix notation
Why Inorder: Matches natural mathematical notation where operators appear between operands
Example:

• Input: Expression tree representing ((3 + 5) * 2)
• Process: Traverse left operand, visit operator, traverse right operand
• Output: “((3 + 5) * 2)” - properly parenthesized infix expression

3. Threaded Binary Tree Construction

Purpose: Creating threading pointers for efficient traversal without recursion or stack
Why Inorder: Threading follows inorder sequence to connect nodes
Example:

• Input: Regular binary tree with nodes [A, B, C, D, E]
• Process: Connect each node’s right pointer to its inorder successor when right child is null
• Output: Threaded tree allowing O(1) space traversal

4. Binary Search Tree Validation

Purpose: Verifying if a binary tree satisfies BST properties
Why Inorder: BST must produce strictly ascending sequence in inorder traversal
Example:

• Input Tree 1: [10, 5, 15, 3, 7, 12, 18] → Inorder: [3, 5, 7, 10, 12, 15, 18] ✅ Valid BST
• Input Tree 2: [10, 5, 15, 3, 7, 12, 6] → Inorder: [3, 5, 7, 10, 6, 12, 15] ❌ Invalid (6 < 10)
• Output: Boolean validation result based on sequence ordering

5. Range Query Processing

Purpose: Finding all values within a specific range in sorted trees
Why Inorder: Natural sorted order allows efficient range processing
Example:

• Input: Customer age BST with range query [25, 35]
• Process: Traverse inorder, collect nodes where 25 ≤ age ≤ 35
• Output: All customers aged 25-35 in sorted order: [26, 28, 31, 34, 35]

6. Database Index Scanning

Purpose: Efficient sequential access to database records in sorted order
Why Inorder: Database B-tree indexes use inorder for range scans
Example:

• Input: Product database with price index
• Process: Inorder scan from $10 to $50 price range
• Output: All products in price order: [$12 Widget, $25 Gadget, $45 Tool]

7. Median & Statistical Operations

Purpose: Finding median, percentiles, and order statistics in BSTs
Why Inorder: Sorted sequence makes statistical calculations straightforward
Example:

• Input: Test scores BST [85, 72, 93, 68, 78, 90, 96]
• Process: Inorder traversal gives sorted scores
• Output: Median = 85 (middle element), 75th percentile = 93

8. Tree Serialization for Reconstruction

Purpose: Saving BST structure in a way that preserves sorting properties
Why Inorder: Combined with preorder/postorder enables efficient BST reconstruction
Example:

• Input: BST with nodes [50, 30, 70, 20, 40, 60, 80]
• Process: Store inorder sequence for sorted data, preorder for structure
• Output: Inorder: [20,30,40,50,60,70,80] + Preorder: [50,30,20,40,70,60,80]

9. Sorted Data Processing

Purpose: Processing data that needs to maintain sorted order during operations
Why Inorder: Eliminates need for separate sorting step
Example:

• Input: Stock price BST updated throughout trading day
• Process: Generate end-of-day report using inorder traversal
• Output: Price movement report in ascending order: [AAPL:$150, GOOGL:$175, MSFT:$200]

10. Successor/Predecessor Finding

Purpose: Locating next/previous elements in sorted order
Why Inorder: Natural sequence makes finding adjacent elements efficient
Example:

• Input: Dictionary BST, find word after “program”
• Process: Use inorder sequence to identify next word
• Output: Successor of “program” is “programming”

⭐ Special Property:

For Binary Search Trees, inorder traversal always produces elements in sorted (ascending) order.

⏱️ Complexity:

• Time: O(n)
• Space: O(h)

---

Postorder Traversal

Postorder traversal is a type of depth-first traversal where the left subtree is processed first, then the right subtree, followed by the current node (root).

Order: Left Subtree → Right Subtree → Root

Think of it as: “Handle my children first, then deal with me”

🔧 Algorithm:

postorder(node):
    if node is not null:
        postorder(node.left)   // 🔄 Traverse left subtree FIRST
        postorder(node.right)  // 🔄 Traverse right subtree SECOND
        visit(node)            // ✅ Process current node LAST

Postorder Result: G → D → E → B → F → C → A

Use Cases & Applications:

1. Tree Deletion & Memory Cleanup

Purpose: Safely deleting tree nodes by removing children before parents
Why Postorder: Children must be deleted before parent to avoid memory leaks and dangling pointers. Dangling pointers mean references to nodes that have already been deleted, which can lead to errors or crashes if accessed later.
Example:

• Input Tree: File system tree with folders and files
• Process: Delete all files first, then empty folders, finally root folder
• Output: Clean memory deallocation: Files → Subfolders → Main folder → Root

2. Postfix Expression Evaluation (Reverse Polish Notation)

Purpose: Evaluating mathematical expressions in postfix notation
Why Postorder: Operands must be processed before operators, matching postfix structure
Example:

• Input: Expression tree for “3 4 + 2 *” (meaning: (3 + 4) × 2)
• Process: Calculate 3, then 4, then +, then 2, finally *
• Output: Result = 14 (first 3+4=7, then 7×2=14)

3. Directory Size Calculation

Purpose: Computing folder sizes by calculating subfolder sizes first
Why Postorder: Must know children sizes before calculating parent size
Example:

• Input: Project folder with subfolders
• Process:

  📄 file1.txt (2KB) 
  📄 file2.java (5KB)
  📁 src/ = 7KB (calculated after files)
  📁 project/ = 7KB (calculated after src/)
  

• Output: Total project size: 7KB

4. Dependency Resolution & Build Systems

Purpose: Processing dependencies before the components that depend on them
Why Postorder: Dependencies must be built/resolved before their dependents
Example:

• Input: Software modules: App depends on Database, Database depends on Logger
• Process: Build Logger first, then Database, finally App
• Output: Build order: [Logger, Database, App]

5. Garbage Collection & Resource Cleanup

Purpose: Cleaning up system resources in proper order
Why Postorder: Child resources must be freed before parent resources
Example:

• Input: Process tree with parent and child processes
• Process: Terminate child processes first, then parent processes
• Output: Clean shutdown without orphaned processes

6. Bottom-up Tree Calculations

Purpose: Computing values that depend on children’s computed values
Why Postorder: Parent calculations need children’s results
Example:

• Input: Employee hierarchy with salary calculations
• Process: Calculate team budgets bottom-up
• Output:

  Employee A: $50K
  Employee B: $60K  
  Manager: $110K (team total)
  Director: $170K (includes manager + own salary)
  

7. Game Object Destruction

Purpose: Destroying game objects and their components in correct order
Why Postorder: Child objects must be destroyed before parent containers
Example:

• Input: Character with weapons, armor, and inventory items
• Process: Destroy items first, then equipment, finally character
• Output: Clean game object removal without references to destroyed objects

8. Abstract Syntax Tree (AST) Code Generation

Purpose: Generating assembly or machine code from expression trees
Why Postorder: Operands must be loaded before operations can be performed
Example:

• Input: Expression tree for “a + b * c”
• Process:

  LOAD b
  LOAD c  
  MULTIPLY
  LOAD a
  ADD
  

• Output: Stack-based code where operands are processed before operators

9. Tree Validation & Structure Checking

Purpose: Validating tree properties by checking children first
Why Postorder: Parent validity often depends on children being valid
Example:

• Input: Binary tree to check if it’s a complete binary tree
• Process: Validate leaf nodes first, then internal nodes, finally root
• Output: Boolean result after checking all subtrees

10. Tree Transformation & Reconstruction

Purpose: Converting tree structures while preserving relationships
Why Postorder: Children must be transformed before parent transformation can occur
Example:

• Input: Parse tree to be converted to different format
• Process: Transform leaf nodes first, then internal nodes, finally root
• Output: Transformed tree maintaining structural integrity

11. UI Component Disposal

Purpose: Properly disposing user interface components and their resources
Why Postorder: Child UI elements must be disposed before parent containers
Example:

• Input: Window with buttons, text fields, and panels
• Process: Dispose buttons and text fields first, then panels, finally window
• Output: Clean UI shutdown without memory leaks

12. Database Transaction Rollback

Purpose: Rolling back nested transactions in reverse order
Why Postorder: Inner transactions must be rolled back before outer transactions
Example:

• Input: Nested transaction tree with savepoints
• Process: Rollback deepest savepoints first, then parent transactions
• Output: Database restored to consistent state before transaction began

⏱️ Complexity:

• Time: O(n)
• Space: O(h)

---

Breadth-First Traversal

Breadth-first traversal (BFS) explores all nodes at the present depth level before moving on to nodes at the next depth level. It uses a queue to keep track of nodes to visit.

Level Order Traversal

Level order traversal is a type of breadth-first traversal where nodes are visited level by level, starting from the root and moving left to right.

Order: Level by level, left to right

Think of it as: “Visit everyone at my level, then go to the next level”

🔧 Algorithm:

levelOrder(root):
    if root is null:
        return
    
    queue = new Queue()
    queue.enqueue(root)
    
    while queue is not empty:
        node = queue.dequeue()
        visit(node)                     // ✅ Process current node
        
        if node.left is not null:       // 📥 Add left child to queue
            queue.enqueue(node.left)
        if node.right is not null:      // 📥 Add right child to queue
            queue.enqueue(node.right)

Level Order Result: A → B → C → D → E → F → G

Use Cases & Applications:

1. Tree Printing & Visualization

Purpose: Displaying tree structure level by level for easy understanding
Why Level Order: Natural visual representation matches how humans perceive hierarchies
Example:

• Input: Company organization tree
• Process: Print CEO first, then VPs, then managers, then employees
• Output:

  Level 0: [CEO]
  Level 1: [VP Sales, VP Engineering]  
  Level 2: [Sales Manager, Dev Manager, QA Manager]
  Level 3: [Sales Rep 1, Sales Rep 2, Developer 1, Developer 2, Tester 1]
  

2. Shortest Path & Minimum Depth Finding

Purpose: Finding shortest distance or minimum steps to reach a target
Why Level Order: BFS guarantees finding shortest path first
Example:

• Input: Family tree, find shortest relationship between two people
• Process: Explore immediate family first, then extended family
• Output: “Alice and Bob are cousins (3 steps apart)” vs “Alice and Charlie are siblings (2 steps apart)”

3. Tree Width & Level Analysis

Purpose: Finding maximum width and analyzing tree structure per level
Why Level Order: Processes entire levels at once for width calculation
Example:

• Input: Website navigation menu tree
• Process: Count items at each menu level
• Output:

  Level 1: 3 main categories (Home, Products, About)
  Level 2: 8 subcategories (max width = 8)
  Level 3: 12 specific pages
  

4. Tree Serialization & Level-wise Storage

Purpose: Storing tree data in level-order format for reconstruction
Why Level Order: Enables breadth-first reconstruction and balanced loading
Example:

• Input: Binary tree [A, B, C, D, E, null, F]
• Process: Store nodes level by level with null markers

• Output: “A

  B,C

  D,E,null,F

  null,null,null,null” (levels separated by

  )

5. Priority Processing & Urgent Task Handling

Purpose: Processing items by priority levels (urgent first, then important, then normal)
Why Level Order: Higher priority levels processed completely before lower ones
Example:

• Input: Hospital patient queue with priority levels
• Process:

  Level 1 (Critical): [Heart Attack, Stroke]
  Level 2 (Urgent): [Broken Bone, Deep Cut]  
  Level 3 (Normal): [Check-up, Vaccination]
  

• Output: All critical patients treated first, then urgent, then normal

6. Game Level Design & Wave Spawning

Purpose: Spawning enemies or challenges in waves/levels
Why Level Order: Each wave must be completed before next wave starts
Example:

• Input: Tower defense game enemy tree
• Process: Spawn Wave 1 enemies, then Wave 2, then Wave 3
• Output:

  Wave 1: [3 Basic Enemies] (must be defeated first)
  Wave 2: [2 Advanced Enemies, 1 Tank] 
  Wave 3: [1 Boss Enemy]
  

7. Educational Content Progression

Purpose: Learning prerequisites where each level builds on previous level
Why Level Order: Students must complete current level before advancing
Example:

• Input: Programming course curriculum tree
• Process:

  Level 1: [Programming Basics]
  Level 2: [Data Types, Variables] 
  Level 3: [Arrays, Functions, Objects]
  Level 4: [Advanced Data Structures]
  

• Output: Sequential learning path ensuring solid foundation

8. Organizational Communication & Announcements

Purpose: Distributing information through hierarchy levels
Why Level Order: Information flows level by level through management chain
Example:

• Input: Company announcement about policy change
• Process: CEO tells VPs, VPs tell Directors, Directors tell Managers, Managers tell employees
• Output: Systematic information distribution ensuring everyone at each level is informed

9. Breadth-First Search in Decision Trees

Purpose: Exploring all options at current decision level before going deeper
Why Level Order: Avoids getting stuck in deep but poor decision paths
Example:

• Input: Investment decision tree
• Process:

  Level 1: [Stocks, Bonds, Real Estate] (explore all first)
  Level 2: [Tech Stocks, Blue Chip | Government Bonds, Corporate Bonds | Residential, Commercial]
  

• Output: Comprehensive analysis of all options at each decision level

10. Network Topology & Router Configuration

Purpose: Configuring network devices level by level from core to edge
Why Level Order: Core routers must be configured before distribution and access layers
Example:

• Input: Corporate network infrastructure
• Process:

  Level 1: [Core Router] (configure first)
  Level 2: [Distribution Switch A, Distribution Switch B]
  Level 3: [Access Switch 1, Access Switch 2, Access Switch 3, Access Switch 4]
  

• Output: Properly configured network with connectivity flowing from core outward

Complexity:

• Time: O(n)
• Space: O(w) - where w is the maximum width of the tree

---

Complete Implementation of Inorder, Preorder, Postorder, and Level Order Traversals

Create a TreeNode Class - The Building Block

import java.util.*;

/**
 * TreeNode represents a single node in our binary tree
 * Think of it as a container that holds data and references to children
 */
class TreeNode<E> {
    E element;              // 📦 The data stored in this node
    TreeNode<E> left;       // ⬅️ Points to the left child
    TreeNode<E> right;      // ➡️ Points to the right child
    TreeNode<E> parent;     // ⬆️ Points to the parent (optional)
    
    // Create a new node with data
    public TreeNode(E element) {
        this.element = element;
        this.left = null;
        this.right = null;
        this.parent = null;
    }
    
    // Create a new node with data and parent reference
    public TreeNode(E element, TreeNode<E> parent) {
        this.element = element;
        this.parent = parent;
        this.left = null;
        this.right = null;
    }
    
    
    // Override toString for easy printing of node data
    @Override
    public String toString() {
        return element.toString();
    }
}

Create a BinaryTree Class to implement all four traversal algorithms

/**
 * BinaryTree implementation with all four traversal methods
 * Supports both recursive and iterative approaches
 */
class BinaryTree<E> {
    private TreeNode<E> root;  // The root of our tree
    private int size;          // Number of nodes in the tree
    
    public BinaryTree() {
        this.root = null;
        this.size = 0;
    }
    
    // Tree Construction Methods
    // Here IllegalStateException is an unchecked exception that indicates the tree already has a root
    // serves as explicit documentation to inform developers about potential exceptions. But it works fine without it.
    public TreeNode<E> addRoot(E element) throws IllegalStateException {
        if (root != null) {
            throw new IllegalStateException("Tree already has a root");
        }
        root = new TreeNode<>(element);
        size++;
        return root;
    }
    
    public TreeNode<E> addLeft(TreeNode<E> parent, E element) {
        if (parent.left != null) {
            throw new IllegalArgumentException("Node already has a left child");
        }
        TreeNode<E> child = new TreeNode<>(element, parent);
        parent.left = child;
        size++;
        return child;
    }
    
    public TreeNode<E> addRight(TreeNode<E> parent, E element) {
        if (parent.right != null) {
            throw new IllegalArgumentException("Node already has a right child");
        }
        TreeNode<E> child = new TreeNode<>(element, parent);
        parent.right = child;
        size++;
        return child;
    }
    
    // Basic Tree Properties
    // These methods provide basic information about the tree structure
    // Not required for all the cases, but useful for understanding the tree
    public TreeNode<E> getRoot() { return root; }
    public int size() { return size; }
    public boolean isEmpty() { return size == 0; }
    
    // PREORDER TRAVERSAL: Root → Left → Right
    // Public method to setup, initialize and call the actual algorithm
    public List<E> preorderTraversal() {
        List<E> result = new ArrayList<>();
        preorderHelper(root, result);
        return result;
    }
    
    // Core algorithm for preorder traversal
    // Recursively visit the root first, then left subtree, then right subtree
    private void preorderHelper(TreeNode<E> node, List<E> result) {
        if (node != null) {
            result.add(node.element);                    // ✅ Visit root first
            preorderHelper(node.left, result);          // 🔄 Then left subtree
            preorderHelper(node.right, result);         // 🔄 Finally right subtree
        }
    }
    
    // INORDER TRAVERSAL: Left → Root → Right
    // Public method to setup, initialize and call the actual algorithm
    public List<E> inorderTraversal() {
        List<E> result = new ArrayList<>();
        inorderHelper(root, result);
        return result;
    }
    

    // Core algorithm for inorder traversal
    // Recursively visit the left subtree first, then root, then right subtree
    private void inorderHelper(TreeNode<E> node, List<E> result) {
        if (node != null) {
            inorderHelper(node.left, result);           // 🔄 Left subtree first
            result.add(node.element);                   // ✅ Then visit root
            inorderHelper(node.right, result);          // 🔄 Finally right subtree
        }
    }
    
    // 🔍 POSTORDER TRAVERSAL: Left → Right → Root
    // Public method to setup, initialize and call the actual algorithm
    public List<E> postorderTraversal() {
        List<E> result = new ArrayList<>();
        postorderHelper(root, result);
        return result;
    }
    
    // Core algorithm for postorder traversal
    // Recursively visit the left subtree first, then right subtree, then root
    private void postorderHelper(TreeNode<E> node, List<E> result) {
        if (node != null) {
            postorderHelper(node.left, result);         // 🔄 Left subtree first
            postorderHelper(node.right, result);        // 🔄 Then right subtree
            result.add(node.element);                   // ✅ Finally visit root
        }
    }
    
    // LEVEL ORDER TRAVERSAL: Level by level
    // Also known as Breadth-First Search (BFS)

    public List<E> levelOrderTraversal() {
        List<E> result = new ArrayList<>();
        if (root == null) return result;
        
        // Start from the root and use a queue to explore each level
        Queue<TreeNode<E>> queue = new LinkedList<>();
        queue.offer(root);
        
        while (!queue.isEmpty()) {
            TreeNode<E> current = queue.poll();
            result.add(current.element);                // ✅ Visit current node and add to result list
            
            // Add children to queue for next level
            if (current.left != null) {
                queue.offer(current.left); // Add left child to queue
            }
            if (current.right != null) {
                queue.offer(current.right); // Add right child to queue
            }
        }
        return result;
    }
    
    // 🎨 Tree Visualization
    public void printTreeStructure() {
        System.out.println("🌳 Tree Structure:");
        if (root == null) {
            System.out.println("(empty tree)");
            return;
        }
        printHelper(root, "", true);
    }
    
    private void printHelper(TreeNode<E> node, String prefix, boolean isLast) {
        if (node != null) {
            System.out.println(prefix + (isLast ? "└── " : "├── ") + node.element);
            
            // 📝 Handle children
            boolean hasLeft = node.left != null;
            boolean hasRight = node.right != null;
            
            if (hasLeft) {
                printHelper(node.left, prefix + (isLast ? "    " : "│   "), !hasRight);
            }
            if (hasRight) {
                printHelper(node.right, prefix + (isLast ? "    " : "│   "), true);
            }
        }
    }
}

🚀 Complete Demo with Practical Examples

public class TreeTraversalDemo {
    
    public static void main(String[] args) {
        System.out.println("BINARY TREE TRAVERSAL ALGORITHMS DEMO");
        System.out.println("Author: Mahedee Hasan");

        //  Creates a string by repeating the double horizontal line character (═) 50 times
        System.out.println("═".repeat(50));
        
        // Build example tree
        BinaryTree<String> tree = buildExampleTree();
        
        // Show tree structure
        // Show original tree in a structured format
        tree.printTreeStructure();
        System.out.println();
        
        // Demonstrate all traversals
        demonstrateTraversals(tree);
        
        // 📊 Show practical applications
        demonstratePracticalApplications();
    }
    
    private static BinaryTree<String> buildExampleTree() {
        // Building this tree:
        //       A
        //      / \
        //     B   C
        //    / \   \
        //   D   E   F
        //  /
        // G
        
        BinaryTree<String> tree = new BinaryTree<>();
        
        TreeNode<String> a = tree.addRoot("A");
        TreeNode<String> b = tree.addLeft(a, "B");
        TreeNode<String> c = tree.addRight(a, "C");
        TreeNode<String> d = tree.addLeft(b, "D");
        TreeNode<String> e = tree.addRight(b, "E");
        TreeNode<String> f = tree.addRight(c, "F");
        tree.addLeft(d, "G");
        
        return tree;
    }
    
    private static void demonstrateTraversals(BinaryTree<String> tree) {
        System.out.println("TRAVERSAL RESULTS:");
        System.out.println("─".repeat(40));
        
        // Preorder traversal
        List<String> preorder = tree.preorderTraversal();
        System.out.println("Preorder  (Root→Left→Right): " + preorder);
        System.out.println("Use case: Tree copying, directory listing");
        // Output: [A, B, D, G, E, C, F]

        // Inorder
        List<String> inorder = tree.inorderTraversal();
        System.out.println("🟩 Inorder   (Left→Root→Right): " + inorder);
        System.out.println("   💡 Use case: BST sorted output, expression trees");
        
        // Postorder
        List<String> postorder = tree.postorderTraversal();
        System.out.println("🟨 Postorder (Left→Right→Root): " + postorder);
        System.out.println("   💡 Use case: Tree deletion, folder size calculation");
        
        // Level Order
        List<String> levelOrder = tree.levelOrderTraversal();
        System.out.println("🟪 Level Order (Top→Bottom): " + levelOrder);
        System.out.println("   💡 Use case: BFS, shortest path, tree printing");
        
        System.out.println();
    }
    
    private static void demonstratePracticalApplications() {
        System.out.println("🎯 PRACTICAL APPLICATIONS:");
        System.out.println("─".repeat(40));
        
        // BST example
        demonstrateBSTSorting();
        
        // Expression tree example
        demonstrateExpressionEvaluation();
        
        // File system example
        demonstrateFileSystemOperations();
    }
    
    private static void demonstrateBSTSorting() {
        System.out.println("📊 Binary Search Tree Sorting:");
        
        BinaryTree<Integer> bst = new BinaryTree<>();
        TreeNode<Integer> root = bst.addRoot(50);
        TreeNode<Integer> left = bst.addLeft(root, 30);
        TreeNode<Integer> right = bst.addRight(root, 70);
        bst.addLeft(left, 20);
        bst.addRight(left, 40);
        bst.addLeft(right, 60);
        bst.addRight(right, 80);
        
        System.out.println("   Input BST: [50, 30, 70, 20, 40, 60, 80]");
        System.out.println("   Inorder:   " + bst.inorderTraversal());
        System.out.println("   ✅ Automatically sorted!");
        System.out.println();
    }
    
    private static void demonstrateExpressionEvaluation() {
        System.out.println("🧮 Expression Tree Evaluation:");
        System.out.println("   Expression: (3 + 5) * 2");
        System.out.println("   Inorder:    3 + 5 * 2     (infix notation)");
        System.out.println("   Postorder:  3 5 + 2 *     (postfix notation)");
        System.out.println("   ✅ Different traversals = Different notations!");
        System.out.println();
    }
    
    private static void demonstrateFileSystemOperations() {
        System.out.println("📁 File System Operations:");
        System.out.println("   Preorder:   List directories before contents");
        System.out.println("   Postorder:  Calculate sizes (children first)");
        System.out.println("   Level Order: Show hierarchy level by level");
        System.out.println("   ✅ Each traversal serves different purposes!");
        System.out.println();
    }
}

📋 Expected Output

🌳 BINARY TREE TRAVERSAL ALGORITHMS DEMO
Author: Mahedee Hasan
══════════════════════════════════════════════════

🌳 Tree Structure:
└── A
    ├── B
    │   ├── D
    │   │   └── G
    │   └── E
    └── C
        └── F

🔍 TRAVERSAL RESULTS:
────────────────────────────────────────
🟦 Preorder  (Root→Left→Right): [A, B, D, G, E, C, F]
   💡 Use case: Tree copying, directory listing
🟩 Inorder   (Left→Root→Right): [G, D, B, E, A, C, F]
   💡 Use case: BST sorted output, expression trees
🟨 Postorder (Left→Right→Root): [G, D, E, B, F, C, A]
   💡 Use case: Tree deletion, folder size calculation
🟪 Level Order (Top→Bottom): [A, B, C, D, E, F, G]
   💡 Use case: BFS, shortest path, tree printing

🎯 PRACTICAL APPLICATIONS:
────────────────────────────────────────
📊 Binary Search Tree Sorting:
   Input BST: [50, 30, 70, 20, 40, 60, 80]
   Inorder:   [20, 30, 40, 50, 60, 70, 80]
   ✅ Automatically sorted!

🧮 Expression Tree Evaluation:
   Expression: (3 + 5) * 2
   Inorder:    3 + 5 * 2     (infix notation)
   Postorder:  3 5 + 2 *     (postfix notation)
   ✅ Different traversals = Different notations!

📁 File System Operations:
   Preorder:   List directories before contents
   Postorder:  Calculate sizes (children first)
   Level Order: Show hierarchy level by level
   ✅ Each traversal serves different purposes!

---

Performance Analysis

📊 Complexity Comparison

Traversal	Time Complexity	Space Complexity	Best Use Case
Preorder	O(n)	O(h)	Tree copying, prefix expressions
Inorder	O(n)	O(h)	BST sorted output, expression trees
Postorder	O(n)	O(h)	Tree deletion, postfix expressions
Level Order	O(n)	O(w)	Level-wise processing, BFS

Where:

• n = number of nodes
• h = height of the tree (O(log n) for balanced, O(n) for skewed)
• w = maximum width of the tree

⚡ Performance Considerations

🔄 Recursive vs Iterative:

Approach	Pros	Cons	Best For
Recursive	✅ Intuitive, clean code	❌ Stack overflow risk	Small to medium trees
Iterative	✅ No stack overflow	❌ More complex code	Large, deep trees

Conclusion

Binary tree traversal algorithms are fundamental building blocks in computer science, providing systematic ways to process tree structures efficiently. Each traversal method has unique characteristics that make it optimal for specific scenarios:

🎯 Key Takeaways:

Algorithm	Strength	Best Application
🟦 Preorder	Root-first processing	Tree copying, directory listing
🟩 Inorder	Natural BST sorting	Sorted data retrieval, expression parsing
🟨 Postorder	Children-first processing	Tree deletion, size calculation
🟪 Level Order	Level-wise exploration	BFS, shortest path, tree printing

💡 Why These Algorithms Matter:

1. Foundation Knowledge: Essential for advanced data structures
2. Problem Solving: Core technique for tree-based problems
3. Performance: Choose right algorithm for optimal efficiency
4. Practical Applications: Used in databases, compilers, file systems
5. Algorithmic Thinking: Develops recursive and iterative thinking skills

🚀 Next Steps for Learning:

• 🌳 Advanced Trees: AVL trees, Red-Black trees, B-trees
• 📊 Graph Algorithms: DFS and BFS on graphs
• 🔄 Dynamic Programming: Tree-based DP problems
• 🎮 Real Projects: Implement file explorers, expression evaluators
• 📈 Optimization: Study cache-efficient traversal techniques

🎓 Academic and Professional Value:

Understanding these algorithms is crucial for:

• 📚 Computer Science Education: Fundamental CS concepts
• 💼 Technical Interviews: Common algorithm questions
• 🏢 Software Development: Building tree-based applications
• 🔬 Research: Foundation for advanced algorithmic research

The mastery of tree traversal algorithms represents a significant milestone in your journey through data structures and algorithms. These techniques will serve as building blocks for more complex algorithms and real-world applications throughout your career in computer science.

Remember: The choice of traversal algorithm should always be based on your specific requirements - there’s no “one size fits all” solution, but there’s always an optimal choice for each scenario! 🎯

---

⬇️ Source code

Connect with me:

• 💼 LinkedIn
• 🐙 GitHub

• 📝 Blog

🌟 Found this helpful? Please share it with others who might benefit from understanding binary tree traversal algorithms. 🌟